Goal

Human body recognition is a core part of interactive applications. A robotic navigation architecture was proposed to allows the robot to navigate in a complex domestic environment without collision [paper]. The authors also proposed an expression of privacy space, a formula incorporating several variables: the distance from the user, the angle of which the user is facing to (i.e., orientation), and the body pose (e.g., sitting down, standing up) of the user. In the paper, these variables were presumed valid and given externally - which are the missing pieces the current research project aims to fill in.

To understand human actions, most research focus on building a prediction model based on modern machine learning approach. While the approach seems promising, they were mostly utilizing the SVM classifier to achieve their goals. Before one can train the SVM classifier, one first needs to obtain an adequate set of training data, define the cues that can reliably extract to and represent the dissimilar characteristics between categories. Usually thousands of images are invloved, which makes this approach very time-/effort-consuming.

In this project, we aim at finding effective measures to address both challenges, human body orientation recognition and posture detection, by making use of position data from Kinect.

Research questions

• Can Kinect effectively detect human body orientation and posture?

Approach

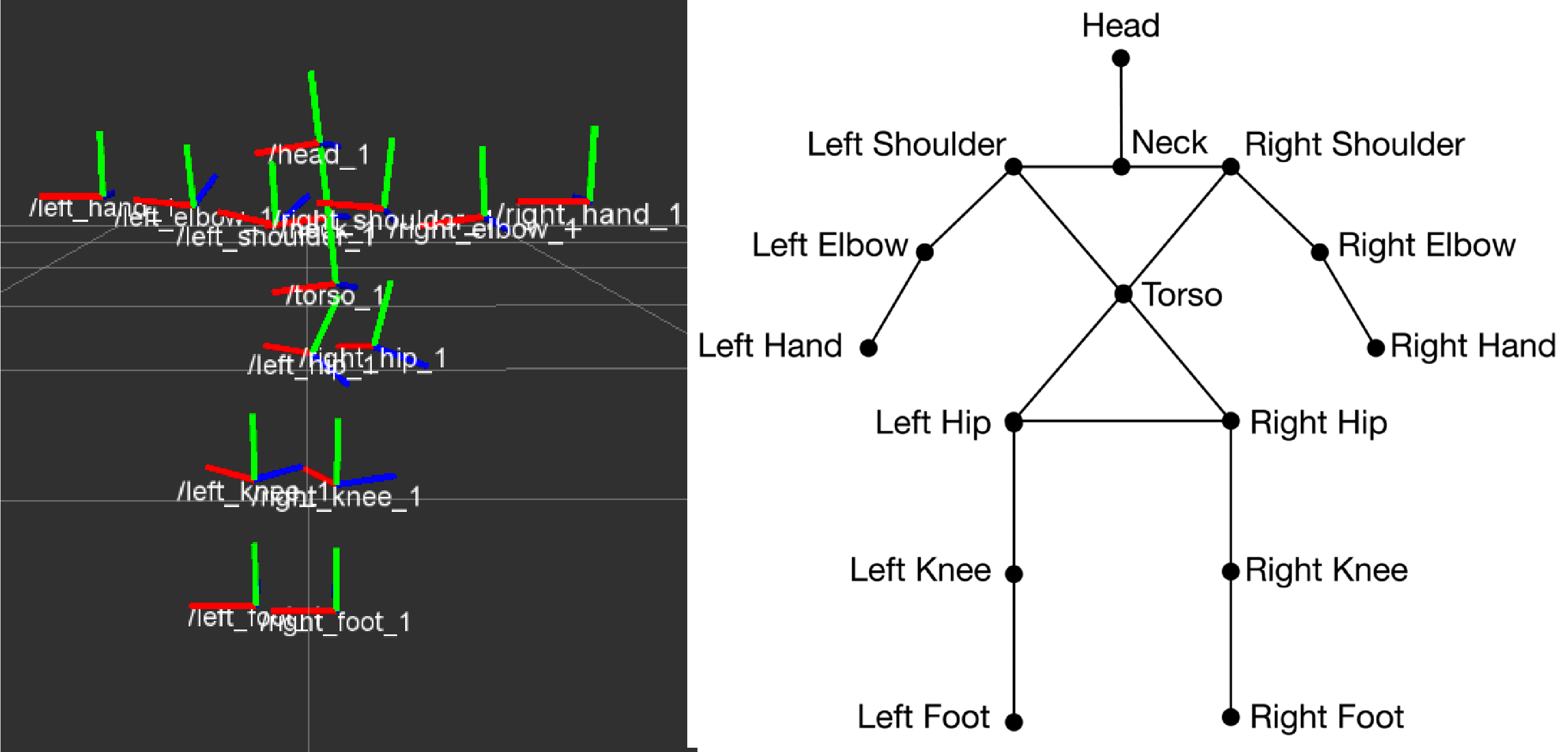
Kinect is the device with two camera sensors: the traditional RGB camera and infrared light sensor which measures depth, position, and motion. With Kinect SDK, we can get coordinate axes for each joint in three colours (red, green and blue), as well as the human skeleton in a stick figure.

Orientation

In the proposed algorithm, only the coordinates of the right and left shoulder and the torso are used. By definition the body orientation is described by the direction the human body facing to. Hence it makes sense to treat body orientation as the vector perpendicular to the body plane. I define the body plane as a plane defined by two vectors “torso to right shoulder” and “torso to left shoulder,” and the body orientation is exactly the normal vector of that plane.

Posture

Model 1: Fixed Angle model

To understand human body pose from the position data in the Kinect system, I first observe the difference in human body image between standing pose and sitting pose, and propose a simple, real-time heuristic, Fixed Angle method. The method intuitively solves this question by measuring the angle between upper and lower body, and classified into standing/sitting pose when the measured angle was larger/smaller than a pre-defined threshold (144 degrees).

Then, to make full use of human body position data from Kinect, I develop another three methods with probability models based on different body measures. The measures include the angle between upper and lower body (\(\theta_{upper\_lower}\)), the ratio between total body length and height (\(r_{BL}\)), and the combination of above two measures.

Notice that in this project, I presume that the data we measured (\(\theta_{upper\_lower}, r_{BL}\)) follow the central limit theorem, and therefore the probability density is normal distributed and can be described as the Gaussian function.

Model 2: statistical model with Angle between upper and lower body

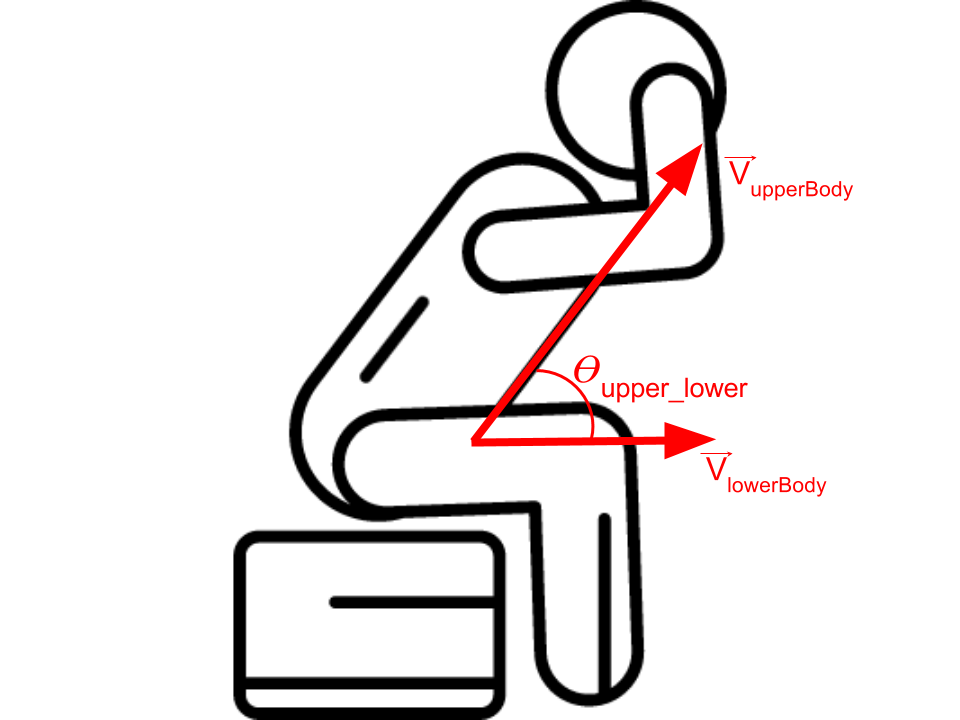The angle between upper body and lower body (\(\theta_{upper\_lower}\)) is defined by the angle between two vectors, the vector “hip to shoulder ” and “hip to knee ”

$$\theta_{upper\_lower}={{\vec{V}_{upperBody}\bullet\vec{V}_{lowerBody}}\over{||\vec{V}_{upperBody}||*||\vec{V}_{lowerBody}||}}$$

With the angle information (\(\theta_{upper\_lower}\)) from subjects for both poses (standing and sitting), I first calculate the mean and standard deviation for both poses, and create the probability models accordingly.

$$P(Standing|\theta_{upper\_lower}=\alpha)=P(\theta_{upper\_lower}=\alpha|Standing)*P(Standing)$$ $$P(Sitting|\theta_{upper\_lower}=\alpha)=P(\theta_{upper\_lower}=\alpha|Sitting)*P(Sitting)$$

$$\Longrightarrow{{P(Standing|\theta_{upper\_lower}=\alpha)}\over{P(Sitting|\theta_{upper\_lower}=\alpha)}}={{P(\theta_{upper\_lower}=\alpha|Standing)}\over{P(\theta_{upper\_lower}=\alpha|Sitting)}}*{{P(Standing)}\over{P(Sitting)}}$$

The posterior probability of each pose for a given measurement (\(\alpha\)) is derived by multiplying the corresponding likelihood with the prior belief of the pose. In many cases it is fair to let \(P(Standing)=P(Sitting)\) when there is no prior preference. However, in some cases, such as on a moving airplane, the probability of sitting would be presumed higher than standing.

Model 3: statistical model with Body Length Ratio

The body length ratio (\(r_{BL}\)) is defined by the ratio between the sum of specific set of body parts (i.e., body length) and the height difference between head and foot (i.e., body height). The ratio is derived with below formula.

$$r_{BL}={{body\ length}\over{body\ height}}={{\sum{BL_i}}\over{h_{head}-h_{foot}}}$$ $$BL_i:length\ of\ body\ part\ i; h_{head}/h_{foot}:height\ of\ head/foot$$ The statistical model is construcred similarly to the Angle model, with the likelihood ratio based on \(r_{BL}\).

Model 4: Hybrid statistical model

Two events are independent if the occurrence of one does not affect the probability of the other, and their joint probability equals the product of their probabilities. Therefore, our hybrid model combines two model mentioned previously (Angle model and Body Length Ratio model), because the two measurements, \(\theta_{upper\_lower}\) and \(r_{BL}\), are independent variables.

Experiment

Participants

Three students with body length 160, 170, 180cm respectively. Two female and one male.

Design

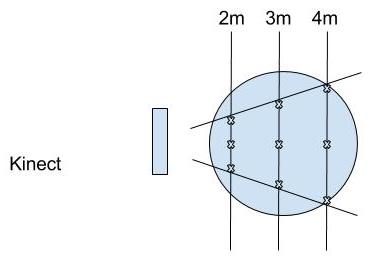
The Kinect was placed on a table with a height of 74cm. There were markings on the floor at 9 positions, three of them were at a near distance (2m), three at the middle distance (3m), and the other three were at the far distance (4m). The spacing interval between positions on the same distance to Kinect was increased from 2m to 4m: the spacing was 1m for the near distance, 1.5m for the middle distance, and 2m for the far distance. At each position, there were tape markings on the floor, indicating different angles with respect to the Kinect. There were 5 line markings for each position, pointing to the direction of 70, 35, 0, -35, -70 degrees respectively, with respect to the Kinect in front.

Materials

hardware

• Kinect V1
• Laptop with Ubuntu (to control Kinect)

software

• ROS (2016) environment
• RVIZ (2016) to visualize Kinect data
• All scripts in ROS were implemented in Python

Measures

• Normal vector of the vector “torso to right shoulder” and “torso to left shoulder”
• \(\theta_{upper\_lower}\)
• \(r_{BL}\)

Procedure

Participants started in a standing post at the center position of 2m distance. The task at each position was composed of facing to the direction of 70 degrees w.r.t. the Kinect for 5 seconds, and turning to 35 degrees for another 5 seconds, and so on for 0, -35, and -70 degrees. Then participants did the same for left position and right position. After finishing all 3 positions (center, left, right) at 2m, participants repeated the tasks for 3m and 4m. Upon finishing all 9 positions in a standing pose, participants were guided to perform the same tasks in a sitting pose. A chair with wheels was provided.

Data analysis

• Probability models were constructed with Microsoft Excel
• Statistical analysis was conducted in Stata

Results & insight

Orientation

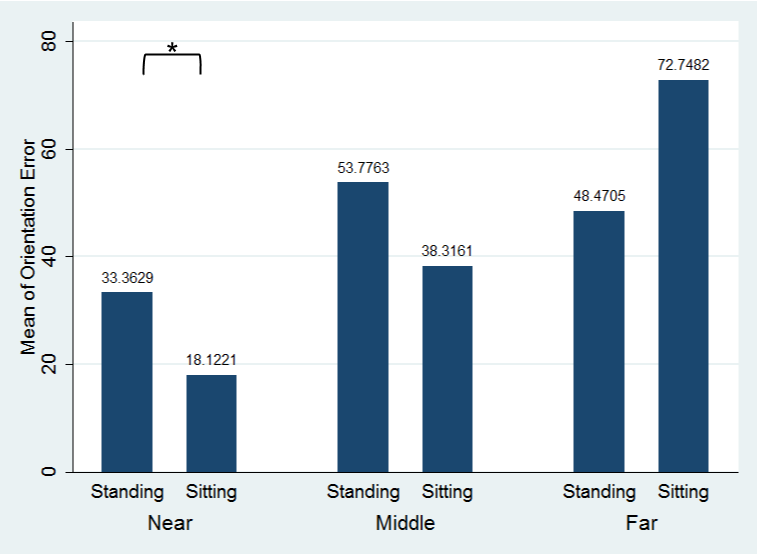
• Kinect performed the best at the center position, near distance (2m), where sitting pose is better than standing pose (...standing pose risks in exceeding FOV (field of vision))
• Kinect is less promising when subjects are facing against Kinect (e.g., facing to the right hand side when Kinect is at the left). (...because Kinect can hardly 'see' the front body)
• To improve the recognition performance, one possibility is to derive front body plane from other vectors; e.g., when the right shoulder is not visible by Kinect, use the vector “torso to head” and “torso to left shoulder” for orientation recognition.

Posture

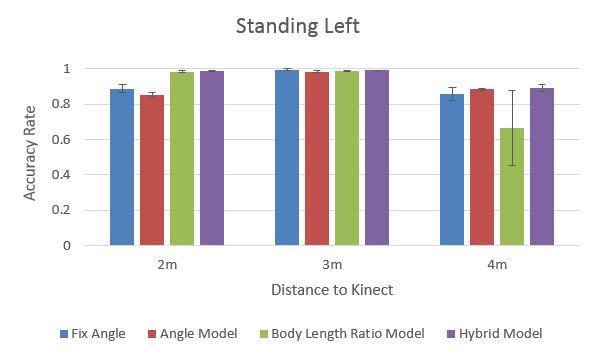
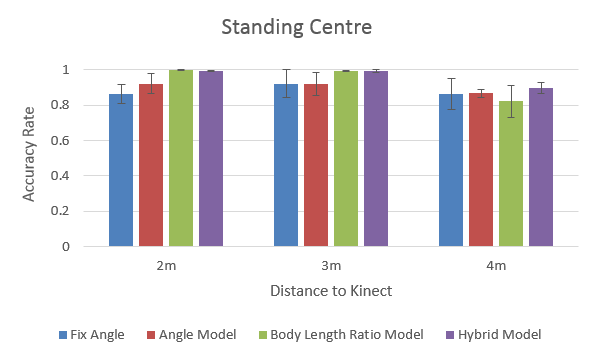
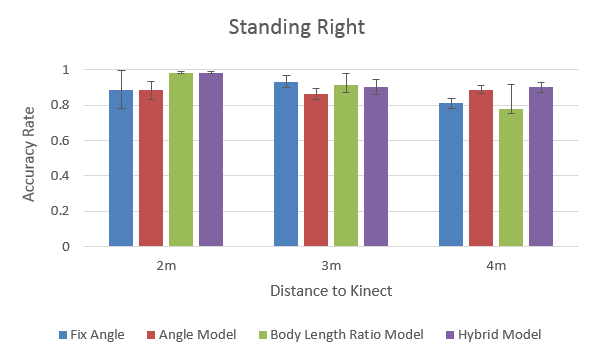
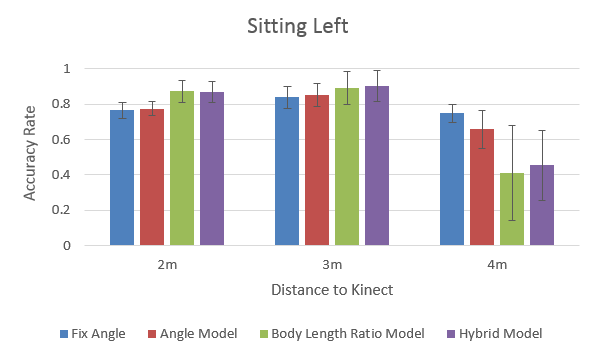
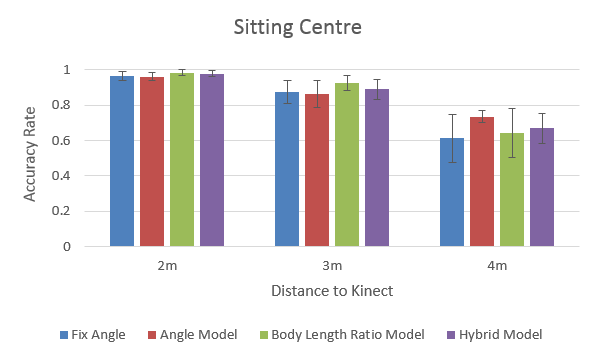
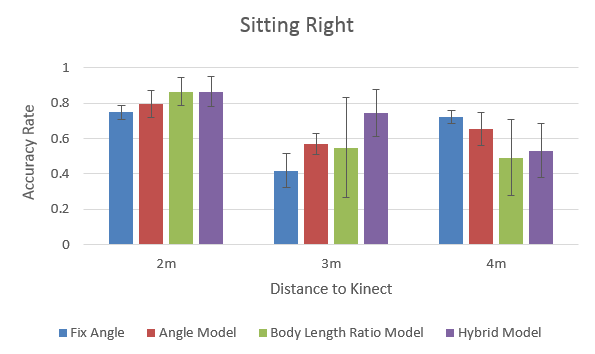
• Kinect has higher pose detection accuracy rate at:
  • near (2m) & middle (3m) distance
  • centre position
  • standing pose
• Hybrid model seems the most robust and promising in general, among all positions and distances.

To dig deeper on how the performance of each method correlates with the distance to Kinect, below is the performance rank:

	Fixed Angle	Angle Model	Body Length Ratio Model	Hybrid Model
Near	3	3	1	1
Middle	1	1	1	1
Far	2	1	4	2

• The “comfort zone” for Kinect: 3m (middle distance). All methods perform quite well at this distance.
• Body Length Ratio model performs quite decent at the near & middle distance, but very poor at the far distance, especially for the sitting pose. (...because Kinect can hardly 'see' body due to the small image size)
• Angle model requires less visual information and its performance is less affected by the increase of distance.
• Hybrid model outperforms other models, except for the far distance (undermined by the Body Length Ratio part).

Conclusion

In this project, I proposed methods tackling two challenges in human action recognition with Kinect, the body orientation recognition and pose detection, by exploiting the geometric information in Kinect system. Compared to the other similar research with SVM classifier, the proposed methods require no training process and data. I also evaluated how the performance of proposed methods vary with different positions, distances, and postures.

For pose detection, while Hybrid model seems to work better in most scenarios, the Angle model performs better in the “harsh” scenarios (e.g., far distance). One can develop a heuristic where the Hybrid model is adopted by default, and switches to the Angle model when an extreme situation is identified.

Team

This is a individual research project by Chia-Kai Yang, and supervised by Dr. Ir. R. H. Cuijpers.